Les mathématiques constituent une science d’étude des quantités, des ordres, des espaces, des nombres et des figures.
SOURCE : http://dms.umontreal.ca/fr/notre-departement/qu-est-ce-que-les-mathematiques
Pourquoi étudier les mathématiques?
Étudier les mathématiques est un excellent choix pour celle ou celui qui a le goût des défis intellectuels et le sens de l'analyse et de l'abstraction. En vous inscrivant en mathématiques, vous entrez dans une filière qui développera vos potentialités intellectuelles, vous apportera la rigueur scientifique et vous ouvrira de nombreuses portes dans des professions stimulantes et variées. Nous vivons dans un monde de science et de haute technologie et une société basée sur l'information, cette société a besoin de mathématiciens.
SOURCE : https://wiki.epfl.ch/info-math/pourquoi
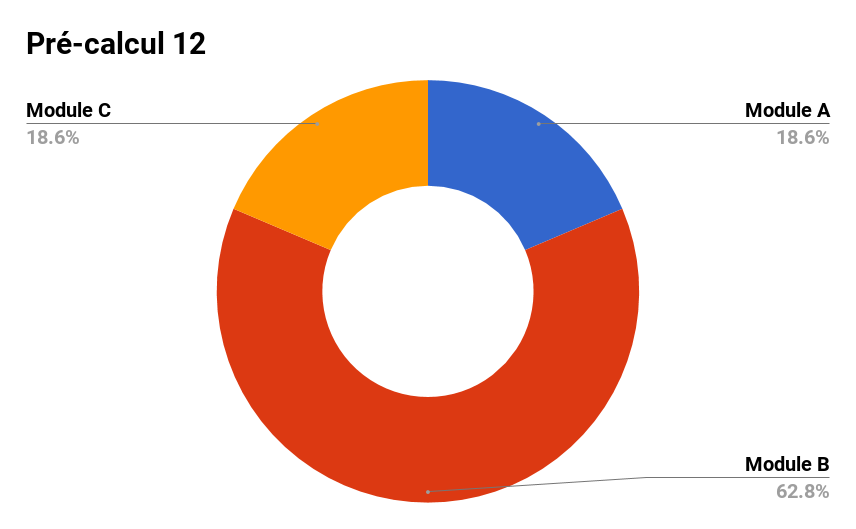
Le contenu du cours
À la fin du semestre, tu seras capable de:
Module A :
- T1. résoudre des problèmes à l’aide des six rapports trigonométriques d’angles exprimés en radians et en degrés.
- T2. représenter graphiquement et analyser les fonctions trigonométriques sinus, cosinus et tangente pour résoudre des problèmes.
- T3. résoudre, algébriquement et graphiquement, des équations trigonométriques du premier et du second degré dont le domaine estexprimé en degrés et en radians.
- T4. démontrer des identités trigonométriques, y compris :
– les identités inverses;
– les identités des quotients;
– les identités de Pythagore;
– les identités de la somme ou de la différence (limité au sinus, au cosinus et à la tangente);
– les identités de l’angle double (limité au sinus, au cosinus et à la tangente).
Module B :
- RF1. démontrer une compréhension de la composition de fonctions et des opérations avec des fonctions.
- RF2. démontrer une compréhension de l’effet des translations verticales et horizontales sur le graphique de fonctions et sur leurs équations respectives.
- RF3. démontrer une compréhension des effets des étirements horizontaux et verticaux sur les graphiques de fonctions et sur leurs équations respectives.
- RF4. appliquer des translations et des étirements aux graphiques de fonctions et à leurs équations respectives.
- RF5. démontrer une compréhension des effets de réflexions (rabattements) sur les graphiques des fonctions et leurs équations respectives, y compris des réflexions (rabattements) par rapport à :
– l’axe des x; – l’axe des y; – la droite y = x. - RF6. démontrer une compréhension des réciproques de relations.
- RF7. démontrer une compréhension des logarithmes.
- RF8. démontrer une compréhension des lois des logarithmes du produit, du quotient et des puissances.
- RF9. tracer le graphique et analyser des fonctions exponentielles et logarithmiques.
- RF10. résoudre des problèmes comportant des équations exponentielles et logarithmiques.
- RF11. démontrer une compréhension de la décomposition en facteurs de polynômes de degré supérieur à 2 (limité aux polynômes de degré ≤ 5 ayant des coefficients entiers).
- RF12. tracer le graphique et analyser des fonctions polynomiales (limité aux fonctions polynomiales de degré ≤ 5).
- RF13. tracer le graphique et analyser des fonctions racine (limité à des fonctions ne contenant qu’un radical).
- RF14. tracer et analyser des fonctions rationnelles (limité à des numérateurs et à des dénominateurs qui sont des monômes, des binômes ou des trinômes).
Module C :
- PC1. appliquer le principe fondamental du dénombrement pour résoudre des problèmes.
- PC2. déterminer le nombre de permutations de n éléments pris r à la fois pour résoudre des problèmes.
- PC3. déterminer le nombre de combinaisons de n éléments différents pris r à la fois pour résoudre des problèmes.
- PC4. effectuer le développement d’un binôme de diverses façons, y compris en ayant recours au binôme de Newton (limité aux exposants qui sont des nombres entiers strictement positifs).